LENGUAJES REGULARES

	INDICE TEMA 2.- LENGUAJES REGULARES

	1.-Definición Lenguaje Regular
		2.-Autómatas finitos	5.- Tipos de autómatas finitos
		3.-Lenguaje asociado al autómata finito	6.- Operaciones sobre AFND
		4.-Representación de los autómatas finitos	7.- Equivalencia entre autómatas

DEFINICIÓN LENGUAJE REGULAR: Al lenguaje generado por medio de una gramática regular. Son aquellos lenguajes cuyas cadenas está formadas por la concatenación de símbolos, en las cuales no hay relación entre una parte de la cadena y otra parte de la cadena.
Vemos que una gramática regular o de tipo 3 es aquella gramática donde las reglas de producción siguen la siguiente estructura: A→ uB o A→ u donde u∈ T^* y A,B∈ V
OBJETIVO: Encontrar reconocedores para los lenguajes regulares. Estos reconocedores se denominan AUTÓMATAS FINITOS.


AUTÓMATAS FINITOS
DEFINICIÓN: Un autámata finito es una quintupla M=(Q,A, d ,q₀,F) en la cual:
Q es un conjunto finito llamado conjunto de estados.
A es un alfabeto llamado alfabeto de entrada.
d es una aplicación de la forma siguiente d : Q x A→ Q de modo que dado un estado y un símbolo del alfabeto se produce otro estado. A esta función se le llama función de transición.
q₀es un elemento de Q, llamado estado inicial.
F es un subconjunto de Q, llamado conjunto de estados finales.
El autómata es un mecanismo con 2 partes:
Una caja negra de control que va evolucionando por los estados del conjunto Q en función del símbolo leído de la cinta.

q₀......................................q_n

Una cinta, ilimitada por la derecha, con una cabeza de lectura que inicialmente se sitúa en la casilla más a la izquierda.

a	b	...	...	...

FUNCIONAMIENTO: En la cinta se escribe la cadena de caracteres de la que queremos determinar si pertenece al lenguaje regular que poseemos. En cada paso el autómata lee un símbolo y segn el estado en el que se encuentre, cambia de estado y pasa a leer el siguiente símbolo. Así hasta acabar de leer todos los símbolos de la cadena, en ese momento si el estado en que está la flecha o cabeza de lectura es un estado final entonces ACEPTA LA CADENA. Si no es un estado final entonces RECHAZA LA CADENA, es decir, la cadena no pertenece a ese lenguaje regular.

LENGUAJE ASOCIADO A UN AUTÓMATA FINITO
El lenguaje que reconoce el autómata está formado por todas aquellas cadenas que se construyen de la siguiente forma: el autómata parte de q₀, lee un símbolo u cualquiera y alcanza un estado final.
Esto se nota de la siguiente forma: L(M)={u∈ A^* / d (q₀,u)∈ F}, donde M es el autómata finito definido como M=(Q,A, d ,q₀,F) .
Ejemplo 1: Qué lenguaje reconoce el autámata dibujado abajo?

Ejemplo 2 :Qué lenguaje reconoce el autómata dibujado abajo?


REPRESENTACIÓN DE LOS AUTÓMATAS FINITOS.-
Existen dos formas de representar los autómatas:
Se representan mediante un Grafo de Transición donde:
Los nodos representan estados, habrá tantos nodos como \|Q\| , cada nodo estará etiquetado por un elemento de Q.
Los arcos representan las transiciones entre los estados. Se etiquetan con el símbolo que corresponde a esa transición.
El estado inicial estará señalado mediante el símbolo → .
Losestados finales estarán señalados mediante el simbolo *, o doble círculo alrededor de la etiqueta del estado final.

EJEMPLO: Realizar el grafo de transición del autómata especificado de la siguiente forma: M=(Q, A, q₀, d , F) donde Q={q₀, q₁, q₂} A={a,b} F={q₂}
	d(q₀,a)=q₁	d(q₀,b)=q₂	d(q₁,a)=q₁	d(q₁,b)=q₂	d(q₂,a)=q₁	d(q₂,b)=q₀


	Con este otro modo de representar los autómatas solamente se especifica la tabla de las transiciones poniendo en la primera fila el alfabeto de entrada y en la primera columna el conjunto de estados Q, de modo que para cada símbolo y estado se asocia un estado al cual se va a ir.

d	A	b
q₀	q₁	q₂
q₁	q₁	q₂
q₂	q₁	q₀


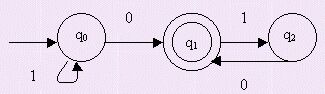
		OPERACIONES SOBRE AUTÓMATAS FINITOS NO DETERMINÍSTICOS: Si tenemos un lenguaje L1 que es aceptado por un autómata finito no determinístico AFND 1 y otro lenguaje L2 que es aceptado por un autómata finito no determinístico AFND2, entonces podemos: Ejemplo: Construir un AFND con TN que reconozca L1�/font>L2 siendo L1={u10v / u, v∈ {0,1}} y L2={u00v /u, v∈ {0,1}} donde sus AFND son los siguientes: AFND 1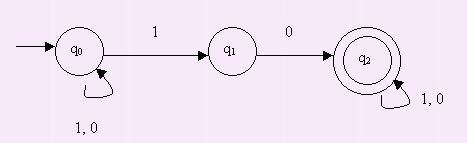 Y AFND2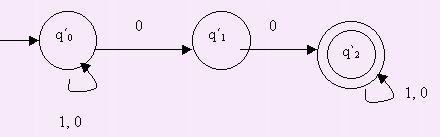
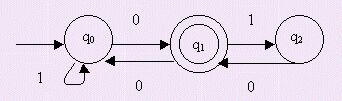
		Ejemplo: Construir un AFND con TN que reconozca la concatenación de L1 y L2

		TIPOS DE AUTÓMATAS FINITOS.-
		AUTÓMATAS FINITOS DETERMINÍSTICOS (AFD)
		AUTÓMATAS FINITOS NO DETERMINÍSTICOS (AFND)
		AUTÓMATAS FINITOS NO DETERMINÍSTICOS CON TRANSICIONES NULAS (AFND CON TN)
		AUTÓMATAS FINITOS NO DETERMINÍSTICOS SIN TRANSICIONES NULAS. (AFND SIN TN)

		DEFINICIÓN: AUTÓMATAS FINITOS DETERMINÍSTICOS (AFD)
		Son aquellos que tienen un número finito de estados, q₀, .....,q_n donde n∈ Ν. Dentro de estos autómatas llamaremos AUTÓMATA FINITO DETERMINÍSTICO MINIMAL a aquel que tiene el menor nmero de estados posibles y sigue reconociendo las cadenas del lenguaje regular.
		EJEMPLO AUTÓMATAS FINITOS DETERMINÍSTICOS
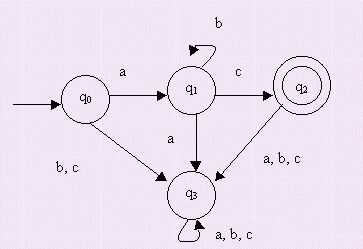
		L={u∈ {a,b,c}* / u=abⁱc i=0}

		DEFINICION :AUTÓMATA FINITOS NO DETERMINÍSTICO (AFND)
		Son aquellos que tienen un nmero finito de estados, q₀, .....,q_n donde n∈ N, y es no deteminístico porque no para todo estado y todo símbolo se tiene una acción a realizar. Es decir de un nodo no pueden salir varios arcos con la misma etiqueta y ni para un nodo existen arcos para todos los símbolos del alfabeto
		EJEMPLO: AUTÓMATA FINITOS NO DETERMINÍSTICO
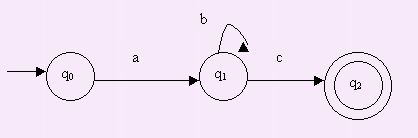
		L={u∈ {a,b,c}* / u=abⁱc i=0}
		DEFINICIÓN :AUTÓMATA FINITOS NO DETERMINÍSTICO CON TRANSICIONES NULAS (AFND CON TN)
		Son aquellos que pueden realizar una transición sin consumir entrada. Estas transiciones se etiquetan con el símbolo de vacíe en el grafo. En la definición, habr�que cambiar la funci� de transición definida como d : Q x A→ Q de la siguiente forma d : Q x (A∪{ε }) →Q. Las transiciones nulas hacen que el autómata pueda quedarse en el estado en el que está o cambiar de estado sin consumir ningn símbolo de la palabra de entrada. Sin embargo el conjunto de lenguajes aceptado por este tipo de autómata es el mismo que para los AFD.
		EJEMPLO AUTÓMATA FINITOS NO DETERMINÍSTICO CON TRANSICIONES NULAS.
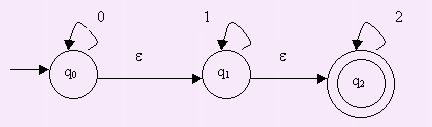
		L={u∈ {0,1,2}* /u=0ⁱ1^j2^k; i,j,k∈ N}

		EQUIVALENCIA ENTRE AUTÓMATA
			EQUIVALENCIA ENTRE AFND CON TN Y AFND.
		Sea un AFND con TN especificado por la quintupla M=(Q,A,q₀,d ,F) el AFND equivalente es M`=(Q`, A`, q₀`,d `,F`) donde:
		Q`=sería el mismo conjunto de estados que se tiene en el AFND con TN, por tanto , Q.
		A`=A.
		q₀`=q0.
		d`(q,u) = conjunto de estados al que se puede pasar leyendo el símbolo u y aquellos estados a los que se llegue mediante ε después o viceversa.
		F`= FU{q₀; si puedes llegar desde el estado q₀ al estado final solamente usando transiciones nulas}
		EJEMPLO: Sea el autómata AFND con TN que reconoce el lenguaje L={aⁱb²ⁿc^jd^k / i,j=0,1, n,k∈/font> N} especificado por la quintupla:
		M=(Q={q₀,q₁,q₂,q₃}, A={a,b,c,d}, d , q₀, F={q₃})
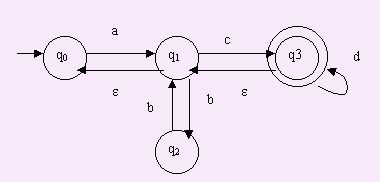		Obtener el AFND.

		EQUIVALENCIA ENTRE AFND Y AFD .
		Sea un AFND especificado por la quintupla M=(Q,A,q₀,d ,F) el AFD equivalente es M`=(Q`, A`, q₀`,d `,F`) donde:
		Q`= conjunto de estados formado por todos los subconjuntos que se puedan formar con los elementos de Q, es decir P(Q).
		A`= el alfabeto del AFND, A.
		q₀`= es el subconjunto de P(Q) que contiene todos los estados iniciales del AFND de partida.
		d`(A,a)= ∪ d(x,a) ∀x ∈ A donde A= subconjunto de estados.
		F`= todos los subconjuntos de estados que contienen al menos un estado final del AFND.
		EJEMPLO: dado el AFND que acepta un lenguaje en el que no aparecen 2 b consecutivas especificado por la quintupla:
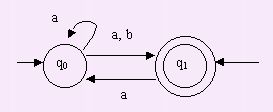
		M=(Q={q₀,q₁}, A={a,b}, {q₀,q₁},d , F={q₁}) Obtener el AFD que acepte ese lenguaje.

EQUIVALENCIA ENTRE AFD Y AFD MINIMAL. ALGORITMO: 1.- Eliminar del AFD los estados innacesibles, es decir, que no se pueden alcanzar, desde el estado inicial. 2.- para cada pareja de estados (q_i, q_l): si uno de los dos estados q_i q_l ∈ F entonces Distinguible(q_i, q_l)=V (verdadero) en una tabla con N estados sin incluir q₀ como filas y como columnas N estados sin incluir el último estado:

3.- Para cada pareja que aún no se ha marcado como V (verdad): (q_i, q_j) entonces 3.1- Para cada símbolo del alfabeto a∈ A. 3.1.1.- Determino que pareja de estados se puede llegar leyendo a (q_i,q_j)→^a (q_k,q_l) 3.1.2.- Si Distinguible (q_k,q_l)=V y q_k≠q_l entonces Distinguible(q_i,q_j)=V también marcamos como distinguibles todas las parejas de la lista asociada a q_i, q_jequivalente L(q_i,q_j) 3.1.3.- Si q_k ≠q_l y Distinguible (q_k,q_l)=F entonces L(q_k,q_l)← {(q_i,q_j)} L(q_k,q_l) 3.1.4.- Si q_k= q_l no se hace nada. Estos pasos se repiten hasta que todas las parejas de estados tengan en la tabla V.

	EJEMPLO DE MINIMIZACION
	Dado el AFD Obtener el AFD minimal.