Los resultados se analizaron en términos de la
media de los errores agrupados por tipo de instancias
y en forma global, para cada valor utilizado de ![]() y
y
![]() .
El error se calcula como:
.
El error se calcula como:
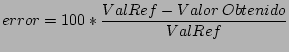 |
(4) |
donde ![]() es el óptimo de la instancia para los
problemas de la mochila con múltiples restricciones (
es el óptimo de la instancia para los
problemas de la mochila con múltiples restricciones (![]() ); y es la cota
de Dantzig (mirar por ej. [24]) para la versión clásica (
); y es la cota
de Dantzig (mirar por ej. [24]) para la versión clásica (![]() ).
).
En la Tabla 1 se muestra la media del error para cada valor de ![]() y cada
y cada
![]() ,
discriminado para las instancias
,
discriminado para las instancias ![]() y
y ![]() .
.
| ||||||||||||||||||||||||||||||||||||||||
Se puede observar que tanto en forma global, como para cada tipo de instancia
en particular, las versiones del algoritmo que usan ![]() obtienen mejores
resultados que los obtenidos con
obtienen mejores
resultados que los obtenidos con ![]() . Esto ocurre para los dos esquemas
de adaptación de
. Esto ocurre para los dos esquemas
de adaptación de ![]() propuestos. También se verifica que para ambos
propuestos. También se verifica que para ambos
![]() 's, un incremento en el valor de
's, un incremento en el valor de ![]() permite reducir el error global
(indicado en la columna
permite reducir el error global
(indicado en la columna ![]() ). Para el caso de decremento, resulta
beneficioso comenzar las mejoras con un operador que cambie 4 bits. Cuando con
4 ya no se obtengan mejoras, se reduce a 3, luego a 2 y finalmente se realiza
un ``ajuste fino'' con
). Para el caso de decremento, resulta
beneficioso comenzar las mejoras con un operador que cambie 4 bits. Cuando con
4 ya no se obtengan mejoras, se reduce a 3, luego a 2 y finalmente se realiza
un ``ajuste fino'' con ![]() .
La adaptación de
.
La adaptación de ![]() en sentido contrario también resulta beneficiosa, aunque
para las instancias
en sentido contrario también resulta beneficiosa, aunque
para las instancias ![]() solo aparecen mejoras respecto a
solo aparecen mejoras respecto a ![]() y no entre los
valores obtenidos cuando se utiliza
y no entre los
valores obtenidos cuando se utiliza ![]() .
.
Es interesante analizar cuanto contribuye cada operador a la obtención del resultado
final. En la Figura 4 se muestran la cantidad de transiciones a soluciones
aceptables (en promedio)
que permitió obtener cada operador para cada valor de ![]() . Los valores obtenidos
se escalaron en el rango
. Los valores obtenidos
se escalaron en el rango ![]() para mejorar la interpretabilidad.
Naturalmente cuando
para mejorar la interpretabilidad.
Naturalmente cuando ![]() ,
todas las mejoras se obtuvieron con
,
todas las mejoras se obtuvieron con ![]() . Es a partir de
. Es a partir de ![]() donde el análisis se
vuelve interesante.
donde el análisis se
vuelve interesante.
En los resultados correspondientes al
![]() que decrementa
que decrementa ![]() , se
observa que cuando
, se
observa que cuando ![]() , prácticamente un
, prácticamente un ![]() de la mejora
se obtuvo con
de la mejora
se obtuvo con ![]() -BitFlip y el restante porcentaje con
-BitFlip y el restante porcentaje con ![]() .
Cuando
.
Cuando ![]() , el
, el ![]() del progreso se debe al uso de
del progreso se debe al uso de
![]() -BitFlip. Del restante
-BitFlip. Del restante ![]() , casi toda la mejora se realiza
con
, casi toda la mejora se realiza
con ![]() -BitFlip. Finalmente cuando
-BitFlip. Finalmente cuando ![]() , el operador
, el operador
![]() -BitFlip es el responsable del
-BitFlip es el responsable del ![]() de los pasos de mejora.
La utilización de
de los pasos de mejora.
La utilización de ![]() y
y ![]() -BitFlip completa prácticamente la
optimización aunque aparecen aproximadamente un
-BitFlip completa prácticamente la
optimización aunque aparecen aproximadamente un ![]() de mejoras
correspondientes a
de mejoras
correspondientes a ![]() -BitFlip.
-BitFlip.
Para el caso de incrementos en ![]() , se observa que para un valor de
, se observa que para un valor de
![]() , hasta un
, hasta un ![]() de mejora se puede conseguir con
de mejora se puede conseguir con ![]() -BitFlip una vez
que la búsqueda se estancó con
-BitFlip una vez
que la búsqueda se estancó con ![]() -BitFlip. Para
-BitFlip. Para ![]() y
y ![]() , los
gráficos muestran que hasta un
, los
gráficos muestran que hasta un ![]() de la mejora corresponde a
de la mejora corresponde a ![]() -BitFlip,
pero luego los operadores subsiguientes pueden mejorar los óptimos locales
encontrados.
-BitFlip,
pero luego los operadores subsiguientes pueden mejorar los óptimos locales
encontrados.
|
También se analizó la media de la cantidad de evaluaciones realizadas
para encontrar el mejor valor, discriminada
en función de ![]() y por tipo de instancia (resultados no mostrados).
y por tipo de instancia (resultados no mostrados).
Cuando se utiliza un esquema de decremento,
para las instancias con múltiples restricciones se observa una reducción de
los valores a medida que aumenta ![]() . Para las instancias del problema clásico,
esta tendencia no se verifica.
En este caso, el valor más alto de evaluaciones se alcanza con
. Para las instancias del problema clásico,
esta tendencia no se verifica.
En este caso, el valor más alto de evaluaciones se alcanza con ![]() .
Luego aparecen los asociados
a
.
Luego aparecen los asociados
a
![]() mientras que el menor valor corresponde a
mientras que el menor valor corresponde a ![]() .
.
Para el esquema de adaptación con incrementos de ![]() , los resultados para
, los resultados para
![]() indican que un aumento de
indican que un aumento de ![]() permite, no sólo obtener mejores
resultados, sino también de forma más rápida. Para
las instancias
permite, no sólo obtener mejores
resultados, sino también de forma más rápida. Para
las instancias ![]() , el valor de
, el valor de ![]() (media de la cantidad de evaluaciones realizadas para obtener la mejor solución) para
(media de la cantidad de evaluaciones realizadas para obtener la mejor solución) para ![]() es el menor de todos,
seguido por
es el menor de todos,
seguido por ![]() y
y ![]() .
.
Naturalmente, esta medida del ``esfuerzo'' no se
puede analizar en forma aislada sino teniendo en mente los resultados obtenidos
en términos del error. Por lo tanto, creemos que las diferencias en la media
del error pueden compensar un posible aumento en las evaluaciones necesarias.