RATIONAL EMBEDDED WAVELET IMAGE CODER

(Version: 4.0: REWIC.HTML v. 4.0 2003/03/06)

Table of Contents

 

Introduction

    REWIC is a software-based implementation of the codec specified in the papers "Rational systems have moderate risk aversion with respect to "gambles" on variable-resolution compression" and "Self-control of quantizers' risk attitude in rational embedded wavelet image coding" by J.A Garcia et al..

   The transmission of large images over (relatively) slow networks is usually done in a progressive fashion. Progressive image transmission schemes should preferably transmit the most significant image information first, so that the user can be presented with a reasonable image approximation already at an early stage of the transmission. At any moment in time a progressive image transmission scheme assigns a priority to the data that has not yet been transmitted at that stage. To achieve an optimal visual approximation on the receiver side at any stage of the transmission this priority should correlate with the visual significance or distinctness of the information.

Let the original image be defined by a set of pixel values $I= \{ x_{i,j} \}$ , where $i,j$ is the pixel coordinate. The coding is actually applied to $C = \Omega ( I)$ , where $\Omega$ represents a unitary hierarchical subband transformation. The 2D array $C = \{ c_{i,j} \} $ has the same dimensions as $I$ . Each element $c_{i,j}$ is called transform coefficient at coordinate $(i,j)$ and can be treated as an integer for the purpose of coding. In an embedded wavelet scheme for progressive transmission, a tree structure, called Spatial Orientation Tree (SOT), naturally defines the spatial relationship on the pyramid that results from the hierarchical subband transformation. Each node of the tree corresponds to a pixel, and its direct descendants (offsprings) correspond to the pixels of the same spatial orientation in the next finer level of the pyramid. Transform coefficients over a spatial orientation tree correspond to a particular local spatial region of the original image, and thus, each SOT is associated with one spatial region.

In rational embedded wavelet coding a decision problem formalizes any situation in which choices are to be made, at any truncation time $t$ , among available SOTs for their transmission, for example by successive approximation quantification. The idea is as follows. Suppose we choose a spatial orientation tree $R_i$ for transmission of a number of its bitstreams, at truncation time $t$ ; then a decoded output occurs and leads to the corresponding consequences (i.e., perceived visual fidelity of the decoded outcome). Thus, the choice of a $R_i$ that is required at any truncation time $t$ produces an outcome (the corresponding set of graylevel occurrences for the decoded output) that is beyond our control and induces a particular set of consequences. The entire transmission of all bit planes for each SOT involves sequential considerations but, this may reduce, essentially, to repeated analysis.

The decision problem of SOT selection at the truncation time $t$ is defined by four elements $\{ {\cal R, G, C}, \preceq \}$ where:

(i)
A set ${\cal R} = \{ R_i, i \in I \}$ of available spatial-orientation trees, one of which is to be selected for transmission of a number of bitstreams $S(R_i,t) $ , at truncation time $t$ ;
(ii)
For each SOT $R_i$ , a set ${\cal G} = \{ G_{l,i} ; l \in L \}$ describing the gray-level occurrences in the spatial region which is reconstructed using the bit streams $S(R_i,t) $ candidates to be transmitted at time $t$ , in addition to bitstreams transmitted, before the time $t$ , for $R_i$ ; where $G_{l,i}$ denotes the uncertain event pixel $X$ within spatial region associated with $R_i$ , taking gray-level value $l$ ;
(iii)
Corresponding to each set $\{ G_{l,i} ; l \in L \}$ , a set of consequences ${\cal C} = \{ c_{l,i} ; l \in L \}$ that induces the transmission of a number of bit streams $S(R_i,t) $ for the particular SOT $R_i$ .
(iv)
$\preceq$ is a preference order between spatial-orientation trees. The relation $\preceq$ expresses the preferences between pairs of available SOTs at a particular truncation time, so that $R_i \preceq R_j$ signifies that $R_i$ is not preferred, at the truncation time, to $R_j$ for further transmission of a number of bitstreams.

A number of coherence axioms were proposed which provide a minimal set of rules to ensure that qualitative comparisons based on $\preceq$ cannot have intuitively undesirable implications. The first axiom states the essence of what is required for an orderly and systematic approach to comparing among spatial-orientations trees: (a) if all consequences were equivalent, there would not be a decision problem; and (b) if the system aspires to make a rational choice between alternative spatial-orientation trees, then it must at least be willing to express preferences between different SOTs.

The second axiom is intended to impose rules of coherence on preference orderings that will exclude possibility of two types of inconsistencies: First, a SOT is strictly preferred to itself; second, willingness to suffer the certain loss of something of value, which the system found itself expressing the preferences $R_i \preceq R_j$ , $R_j \preceq R_k$ , and $R_k \preceq R_i$ among the three SOTs $R_i, R_j$ , and $R_k$ .

The binary relation $\preceq$ may also provide a qualitative basis for comparing, by extension, consequences and gray level occurrence events. And the third axiom shall ensure the consistency of any kind of preferences (e.g., between consequences or graylevel occurrence events).

We also need to introduce some form of quantification by setting up a standard unit of measurement such that enables the transmission system to assign a numerical value to any given SOT in the selection problem. In short, precision through quantification is achieved by introducing some form of numerical standard into the system already equipped with a coherent qualitative ordering relation (the first three axioms). We shall regard it as essential to be able to aspire to some kind of quantitative precision in the context of comparing spatial-orientation trees. It is therefore necessary that we have available some form of standard SOTs. This notion of quantification is given by means of two additional axioms.

The sixth postulate states the assumption that the statistical characterization of the decoded output involving information transmitted over $R_i$ up to this time is independent of the particular characterization of the output corresponding to another SOT $R_j$ .

The seventh axiom invokes another specific preference pattern that may arise in the SOT selection process at any truncation time: The proportion of remaining data in $R_i$ still not delivered to the decoder which the transmission system is willing to give up at truncation time $t$ for an improvement in information transmitted over $R_j$ does not depend on the absolute amount of remaining information in $R_i$ involved.

Let $q_{l,i} $ be the probability of gray level $l$ in the region that was reconstructed using the bit streams transmitted for the region $R_i$ , before time $t$ ; also, $ p_{l,i}$ be the probability of gray level $l$ in the region that was reconstructed using the bit streams $S(R_i,t) $ , in addition to those transmitted for $R_i$ before time $t$ . In a rational transmission system for which these seven axioms hold, the possible functional forms of the expected increase in utility provided by the transmission at time $t$ of bit streams $S(R_i,t) $ , given an initial probability distribution ${\cal Q} \equiv \{ q_{l,i}; l \in L\}$ that is strictly positive, are as follows:

\begin{eqnarray*} I( S(R_i,t) / {\cal Q} ) = \left\{ \begin{array}{ll} \sum_{l}... ...} \right)^r \right] & \mbox{ if $ r > 0$} \end{array} \right. \end{eqnarray*}



where the system exhibits a risk seeking posture with respect to ``gambles'' on SOT-dependent quality of encoding when $r > 1$ , whereas $r< 1$ implies risk aversion. The risk neutrality is given by $r=1$ .

Therefore, in accordance with the seven postulates, the rational choice for transmission at truncation time $t$ is to select bit streams $S(R_{\dag },t)$ that provide the maximum achievable expected increase in utility $I(S(R_i,t) / {\cal Q} )$ per coding bit, over available spatial-orientation trees $R_i$ :

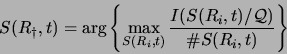
\begin{displaymath} S(R_{\dag },t) = \arg \left\{ \max_{S(R_i,t)} \frac{ I(S(R_i,t) / {\cal Q} )}{\char93 S(R_i,t)} \right\} \end{displaymath} (1)

where $\char93 S(R_i,t)$ denotes the number of bits in $S(R_i,t) $ .

The information prioritization in progressive transmission is a noncooperative decision problem among competing quantizers (e.g., spatial orientation trees) at successive truncation times. This is so because in prioritization the target bitrate may be unknown and then every competing quantizer wants to be selected to transmit first at the present truncation time, aware that might be the last one. Since the information prioritization is seen as a noncooperative decision by any quantizer, they very possibly do not accept any of the restrictions under what a group of cooperative quantizers are to rationally agree on a joint allocation of bits up to a target rate. Anyway, there exists some property of a general solution for cooperative action which can naturally be accepted by noncooperative quantizers. And this property shall play a key role in the estimation of the risk attitude for quantizers in the selection problem.

Firstly, we need to introduce the notion of self-control in risk attitude as follows: A transmission system that prioritizes the bitstream corresponding to the maximum achievable benefit per coding bit over available quantizers, has self-control of risk attitude if the quantizers' risk aversion parameter is selected, at each truncation time, in the range of moderate risk aversion to minimize the maximum difference in benefit per coding bit between quantizers, with the benefit being the expected increase in utility.

The reason to select the risk attitude in the range of the moderate risk aversion comes from the fact that, even though a rational system for progressive transmission might exhibit either a risk seeking posture or risk aversion with respect to ``gambles'' on variable-resolution compression, at moderate risk aversion (i.e., $r$ around $0$ ) a rational embedded wavelet coder is best able to maintain acceptable image fidelity.

The additional property of a rational transmission system with self-control of risk attitude is that, at every truncation time, quantizers are willing to sacrifice some potential gain in the magnitude of the benefit corresponding to any bit allocation in order to prevent, to the maximum extent possible in the range of moderate risk aversion, any of the other quantizers from receiving disproportionately large gains in benefit. As a result, a rational transmission system with self-control of risk attitude integrates, in the range of moderate risk aversion, the solution of a noncooperative decision model for rational prioritization with the solution of a general procedure for cooperative distribution.
    This research was sponsored by the Spanish Board for Science and Technology, (CICYT) under grant TIC2000-1421.

(This is an old version of REWIC software)

Go to the last version of REWIC software